TOC
本文是极客时间中数据结构与算法课程的笔记,包含数据结构和基础算法
复杂度分析
- 时间复杂度
- 空间复杂度
不同情况下,同一段代码的时间复杂度可能是不一样的。这时候需要以下三个:
- 最好情况时间复杂度,就是在最理想情况下,执行这段代码的时间复杂度。
- 最坏情况时间复杂度,在最糟糕的情况下,执行这段代码的时间复杂度。
- 平均情况时间复杂度,也就是概率论中的加权平均值,也叫期望值,所以也叫加权平均时间复杂度或者期望时间复杂度
另外还有一个更高级的均摊时间复杂度
对一个数据结构进行一组连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候我们就可以将这一组操作放在一块分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他时间复杂度比较低的操作上。而且,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度。
线性表(Linear list)
线性表 就是数据排成一条线一样的结构。每个线性表上的数据最多只有前和后两个方向
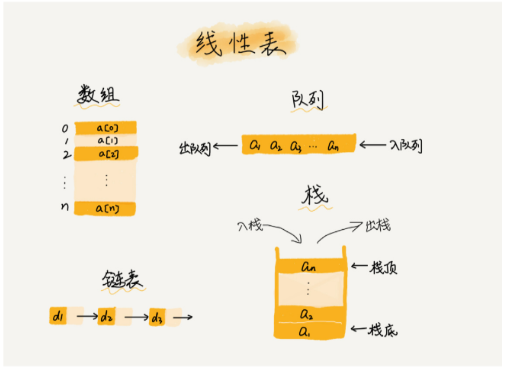
数组
从数组存储的内存模型上来看,“下标”最确切的定义应该是“偏移(offset)”,相当于首地址的偏移
面试常见:数组和链表区别
数组支持随机访问,根据下标随机访问的时间复杂度为O(1)
低效的”插入“和”删除“ - “插入”-替换到最后,这样就不用全部右移。快排就是用了这个思想 - “删除”-标记再一起删除
链表 (Linked list)
缓存淘汰算法
- 先入先出策略 FIFO(First in,First out)
- 最少使用策略 LFU(Least Frequently Used)
- 最近最少使用策略 LRU(Least Recently Used)
分类:单链表、双向链表(LinkedHashMap,空间换时间,再联想到缓存)、循环链表
特点:
插入和删除都是O(1)的时间复杂度
随机访问只能依次遍历,时间复杂度为O(n)
思考题:如何判断字符串是否回文?
快慢指针算法快速找到单链表中间值
普通方法就是遍历两次,第一次遍历得到链表长度,第二次遍历得到中间值。时间复杂度为1.5n。(这里需要强调1.5) 快速链表方法就是利用两个指针,慢指针每次移动一个数据,快指针每次移动两个数据。最外层的循环用快指针。当快指针遍历完后,内层慢指针刚好循环到一半。时间复杂度为0.5n。代码如下:
class GetMidVaule(LinkList L, elmType *e){ LinkList k,m; k=m=L; for(int i=0;k.next!=null;i++){ k=k.next.next; m=m.next; } *e=m.data; }从中间节点对后半部分逆序,或者将前半部分逆序
一次循环比较,判断是否回文
恢复现场
//TODO 代码实现
如何轻松写出正确的链表代码?:
前提:写好链表代码不容易,复杂的比如链表反转、有序链表合并,广大面试者中写好的不足10%
技巧:
理解指针或引用的含义
将某个变量赋值给指针,实际上就是将这个变量的地址赋值给指针,或者反过来说,指针中存储了这个变量的内存地址,指向了这个变量,通过指针就能找到这个变量
警惕指针丢失和内存泄漏
插入结点时,一定要注意操作的顺序。删除结点时,一定要记得手动释放内存空间。java不需要
利用哨兵简化实现难度
针对链表的插入、删除操作,需要对插入第一个结点和删除最后一个结点的情况进行特殊处理
重点留意边界条件处理
举例画图,辅助思考
多写多练,没有捷径
练习
- 单链表反转
- 链表中有环的检测
- 两个有序的链表合并
- 删除链表倒数第n个结点
- 求链表的中间结点
写链表代码是最考验逻辑思维能力的。链表代码写的好坏,可以看出一个人写代码是否够细心,考虑问题是否全面。
栈
栈是一种“操作受限”的线性表,只允许在一端插入和删除数据。
顺序栈和链式栈
- 顺序栈:用数组实现的栈,我们叫做顺序栈
- 链式栈:用链表实现的栈,我们叫做链式栈
栈的应用
- 函数调用中的,函数调用栈
- 编译器利用栈来实现表达式求值
- 栈在括号匹配中的应用
队列
队列跟栈一样,也是一种操作受限的线性表数据结构
顺序队列和链式队列
循环队列
阻塞队列和并发队列
阻塞队列其实就是在队列的基础上加了阻塞操作。 简单来说,就是在队列为空的时候,从队头取数据会被阻塞,直到队列中有了数据才能返回; 如果队列已满,那么插入操作就会被阻塞,直到队列中有空闲位置后再插入数据。
上述的定义就是一个“生产者-消费者模型”!
线程安全的队列我们叫作并发队列。最简单的实现方式是直接在enqueue(),dequeue()方法上加锁,但是锁力度大并发度会比较低,同一时刻仅允许一个存或者取操作。实际上,基于数组的循环队列,利用CAS原子操作,可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。
在实战篇将Disruptor的时候,我们再详细讲并发队列的应用。
递归
从我个人学习数据结构与算法的经历来看,有两个最难理解的知识点,一个是动态规划,另一个就是递归。学会递归非常重要,比如DFS深度优先搜索、前中后序二叉树遍历等等。
递归需要满足的三个条件
- 一个问题的解可以分成几个自问题的解
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
- 存在递归终止条件
如何编写递归代码?
最关键的是写出递推公式,找到终止条件,剩下将递推公式转化成代码就很简单了
假如这里有n个台阶,每次你可以跨1个台阶或者2个台阶,请问走这n个台阶有多少种走法?如果有7个台阶,你可以2,2,2,1 这样子上去,也可以 1,2,1,1,2 这样子上去,总之走法有很多,那如何用编程求得总共有多少种走法呢?
我们仔细想下,实际上,可以根据第一步的走法把所有走法分为两类,第一类是第一步走了 1 个台阶,另一类是第一步走了 2 个台阶。所以n个台阶的走法就等于先走 1 阶后,n-1 个台阶的走法 加上 先走 2 阶后,n-2 个台阶的走法。用公式表示就是:
f(n) = f(n-1)+f(n-2)
有了递推公式,递归代码基本上就完成了一半。用小点的数得出递归终止条件就是f(1)=1,f(2)=2.
我们把递归终止条件和刚刚得到的递推公式放到一起就是这样的:
f(1)=1;
f(2)=2;
f(n)=f(n-1)+f(n-2);
转化成递归代码
int f(int n) {
if(n == 1) return 1;
if(n ==2 ) return 2;
return f(n-1)+f(n-2);
}
写递归代码的关键就是找到如何将大问题分解为小问题的规律,并且基于此写出递推公式,然后再推敲终止条件,最后将递推公式和终止条件翻译成代码
只要遇到递归,我们就把它抽象成一个递推公式,不用想一层层的调用关系,不要试图用人脑去分解递归的每个步骤
容易出的问题
- 堆栈溢出
- 重复计算
调试递推代码
- 打印日志发现,递归值
- 结合条件断点进行调试
排序
| 章节 | 排序算法 | 时间复杂度 | 是否基于比较 |
|---|---|---|---|
| 11 | 冒泡、插入、选择 | On的平方 | 是 |
| 12 | 快排、归并 | O(nlogn) | 是 |
| 13 | 桶、计数、基数 | O(n) | 否 |
基本的排序
插入排序-优化(希尔排序)
思考:一个有序数组,我们往里面添加一个新的数据后,如何继续保持数据有序呢?很简单,我们只要遍历数组,找到数据应该插入的位置将其插入即可。
左侧未已排序区间,右侧为未排序区间;两种操作,一种是元素的比较,一种是元素的移动。
冒泡排序
只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复n次,就完成了n个数据的排序工作。
选择排序
选择排序算法的实现思路类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
分治思想 O(nlogn)
- 归并排序-待学习
- 快速排序-待学习
线性排序(Linear sort),不基于比较
- 桶排序
- 计数排序
- 基数排序
如何实现一个通用的排序方法
二分查找
最简单的情况
有序数据中不存在重复元素 可以用循环和递归两种方式实现
二分查找的局限性
- 首先,二分查找依赖的是顺序表结构,也就是数组
- 其次,二分查找针对的是有序数据
- 再次,数据量太小不适合用二分查找,顺序遍历足够
- 最后,数据量太大也不适合用二分查找,要求有很大的连续的内存空间
三个容易出错的地方
- 循环退出条件
- mid的取值
- low和high的更新
跳表
为链表建立多级索引的结构叫做跳表
散列表
散列表用的就是 数组支持按照下标访问的时候,时间复杂度为O1的特性。 通过散列函数,将键值转化为数组下标,从对应的数组下标位置取数据。
两个核心问题
- 散列函数设计
- 散列冲突解决
- 开放寻址法(线性探测、二次探测、双重散列)
- 链表法
工业级别的散列表
哈希算法
- 应用一:安全加密
- MD5
- SHA
- DES
- AES
- 应用二:唯一标识
- 应用三:数据校验
- 应用四:散列函数
- 应用五:负载均衡
- 应用六:数据分片
- 应用七:分布式存储(一致性哈希)