TOC
本文是极客时间中数据结构与算法课程的笔记,包含一些高级算法和实际场景
非线性表
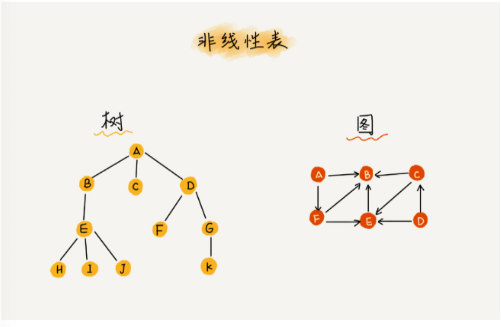
二叉树
类型
- 满二叉树:叶子节点全部在最底层,除了叶子节点,每个节点都有左右两个子节点
- 完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其它层的
存储方法
- 链式存储法
- 顺序存储法
遍历
- 中序遍历
- 先序遍历
- 后序遍历
查找树
二叉查找树(Binary Search Tree,BST)
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都小于这个节点的值,而右子树节点的值都大于这个节点的值。 缺陷:特殊情况下会退化成链表
平衡二叉查找树
- 平衡二叉查找树,比如AVL树、红黑树、Splay Tree(伸展树)、Treap(树堆)
- 发明平衡二叉查找树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题
散列表的插入、删除、查找操作的时间复杂度都可以做到常量级的O(1),非常高效。而二叉查找树在比较平衡的情况下,插入、查找操作时间复杂度才是O(㏒n),相对散列表,好像并没有什么优势,那我们为什么还要用二叉查找树?
- 散列表中的数据无序存储
- 散列表扩容耗时很多
- 因为哈希冲突的存在和哈希函数的耗时,也不一定比平衡二叉查找树的效率高
- 散列表的构造比二叉查找树要复杂,比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
- 最后,为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
综上所述,平衡二叉查找树在某些方面还是优于散列表,所以,这两者的存在并不冲突。需要结合具体的需求来选择使用哪一个。
红黑树
递归树
堆和堆排序:为什么说堆排序没有快速排序快?
首先,堆是一种特殊的树。满足以下两点,它就是一个堆:
- 堆是一个完全二叉树
- 堆中每一个节点的值,都必须大于等于(或小于等于)其子树中每个节点的值。
解释:
第一点,堆必须是一个完全二叉树。完全二叉树要求,除了最后一层,其它层的节点个数都是满的,最后一层的节点都靠左排列。
第二点,堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值。实际上,换个说法,堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫做“小顶堆”。
如何实现一个堆?
完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。
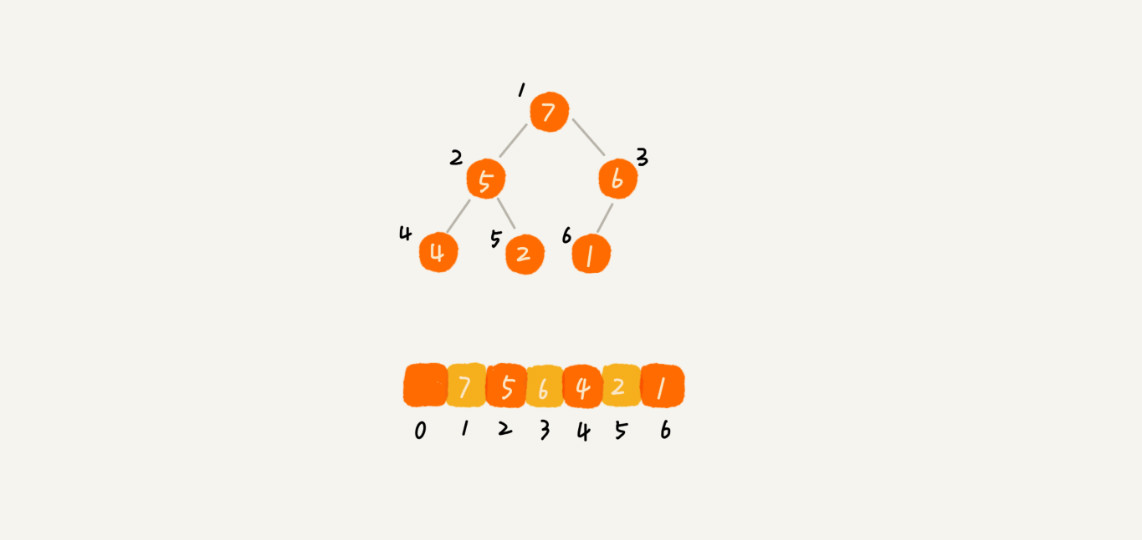
从图中我们可以看到,数组中下标为i的左右子节点,就是下标为 i*2 的节点,右节点就是下标为 i*2+1 的节点,父节点就是下标为 i/2 的节点。
1.往堆中插入一个元素(堆化:heapify)
就是顺着节点所在的路径,向上或者向下,对比,然后交换。
我们可以让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系,我们就互换两个节点。一直重复这个过程,直到父子节点之间满足刚说的那种大小关系。这就是从下往上的堆化方法。
我们把最后一个节点放到堆顶,然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。
2.删除堆顶元素
3.如何基于堆实现排序?
时间复杂度非常稳定,是O(nlogn),并且还是原地排序算法。
两个大步骤:建堆和排序
建堆
第一种是借助之前,在堆中插入一个元素的思路。尽管数组中包含n个数据,但是我们假设,起初堆中只包含一个数据,就是下标为 1 的数据。
第二种实现思路,截然相反。第一种思路是从前往后处理数组数据,并且每个数据插入堆中时,都是从下往上堆化。 排序
为什么快速排序比堆排序性能好?
- 堆排序数据访问的方式没有快速排序好,是跳着访问的。
- 对于同样的数据,在排序过程中,堆排序算法的数据交换次数要多于快速排序。
堆的应用:如何快速获取到Top 10最热门的搜索关键词?
图
顶点、边、度、入度出度
邻接矩阵存储方法
邻接矩阵的底层依赖一个二维数组。对于无向图来说,如果顶点 i 与顶点 j 之间有边,我们就将 A[i][j] 和 A[j][i] 标记为 1;对于有向图来说,如果顶点 i 到顶点 j 之间,有一条箭头从顶点 i 指向顶点 j 的边,那我们就将 A[i][j] 标记为 1。同理,如果有一条箭头从顶点 j 指向顶点 i 的边,我们就将 A[j][i] 标记为 1。对于带权图,数组中就存储相应的权重。
邻接矩阵,稀疏图会浪费空间
邻接表存储方法
每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。另外我需要说明一下,图中画的是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。对于无向图来说,也是类似的,不过,每个顶点的链表中存储的,是跟这个顶点有边相连的顶点,你可以自己画下。
邻接矩阵存储起来比较浪费空间,但是使用起来比较节省时间。
相反,邻接表存储起来比较节省空间,但是使用起来就比较耗时间。
图的表示:如何存储微博、微信等网络社交重的三度好友关系
深度(DFS)和广度优先搜索(BFS)
我们知道,算法是作用于具体数据结构之上的,深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构的。这是因为,图这种数据结构的表达能力很强,大部分涉及搜索的场景都可以抽象成“图”。
图上的搜索算法,最直接的理解就是,在图中找出从一个顶点出发,到另一个顶点的路径。具体方法有很多,比如今天要讲的两种最简单、最“暴力”的深度优先、广度优先搜索,还有 A、IDA 等启发式搜索算法。
总结
广度优先搜索,通俗的理解就是,地毯式层层推进,从起始顶点开始,依次往外遍历。广度优先搜索需要借助队列来实现,遍历得到的路径就是,起始顶点到终止顶点的最短路径。
深度优先搜索用的是回溯思想,非常适合用递归实现。换种说法,深度优先搜索是借助栈来实现的。在执行效率方面,深度优先和广度优先搜索的时间复杂度都是 O(E),空间复杂度是 O(V)。
字符串匹配
比如java中的indexOf(),Python中的find()函数等,它们底层就是以来接下来要讲的字符串匹配算法
BF算法
全称是 Brute force,也叫朴素匹配算法
RK算法
是BF算法的改进,巧妙的借助了哈希算法,让匹配的效率有了很大的提升。
BM算法
KMP算法
Trie树
像Google、百度这样的操作引擎,它们的关键词提示功能非常全面和精准,肯定做了很多优化,但底层最基本的原理就是这种数据结构:Trie树
Trie树,也叫“字典树”,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
其他解决方法,比如散列表、红黑树,或者前面的字符串匹配算法
Trie树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起
AC自动机
如何实现一个高性能的敏感词过滤系统呢?这就要用到多模式串匹配算法
之前的BF算法、RK算法、BM算法、KMP算法都是单模式串匹配算法,Trie树是多模式串匹配算法